The Physics behind Kernel GANs

Introduction

This project started as an attempt to understand what happens to GAN training dynamics in the overparameterized regime. The theory behind the neural tangent kernel (Jacot et al. 2018) had already been applied to discriminative models such as RNN (Alemohammad et al. 2020, Emami et al. 2021) and ResNets (Huang et al. 2020). However much less exploration had been done with generative models.

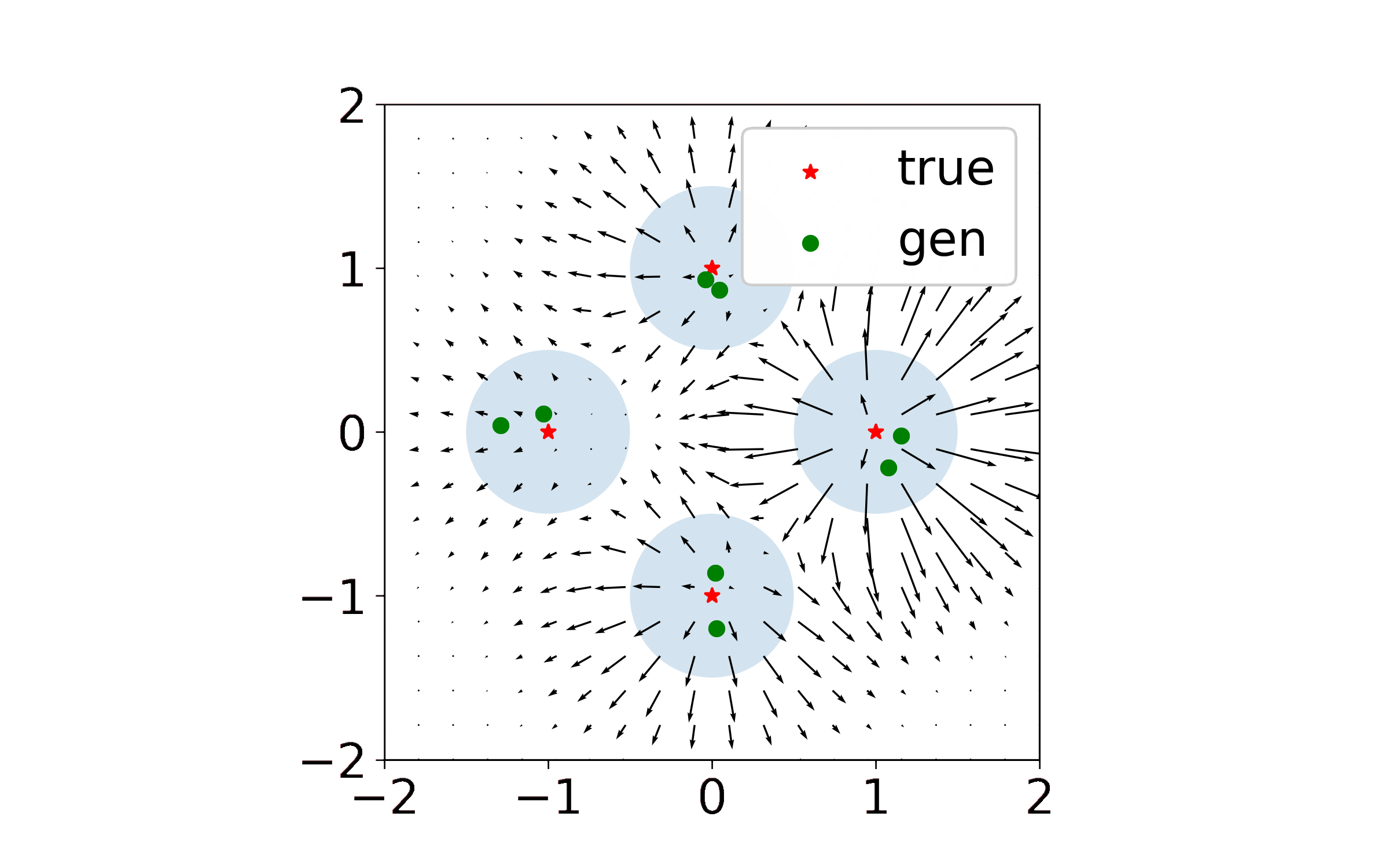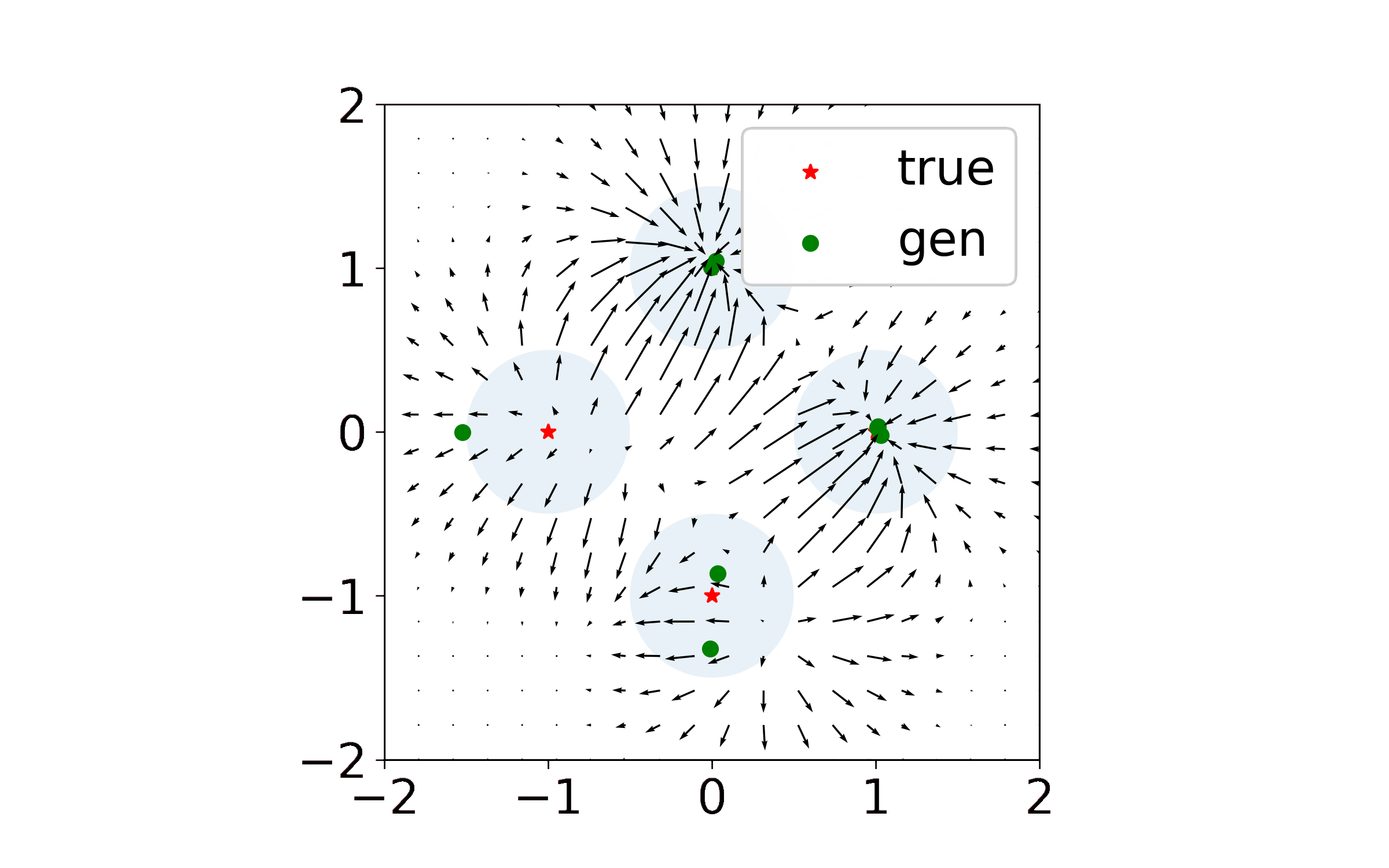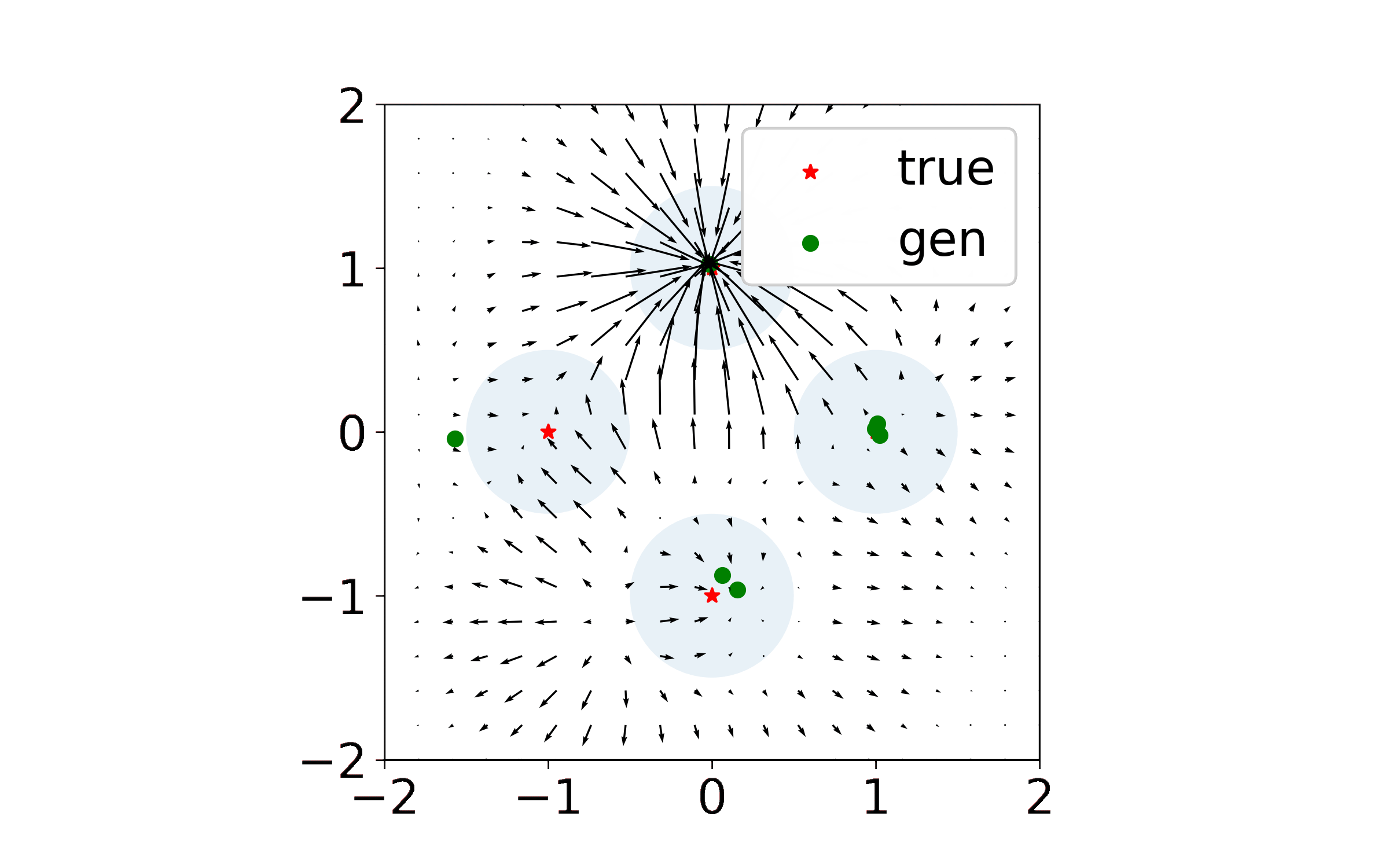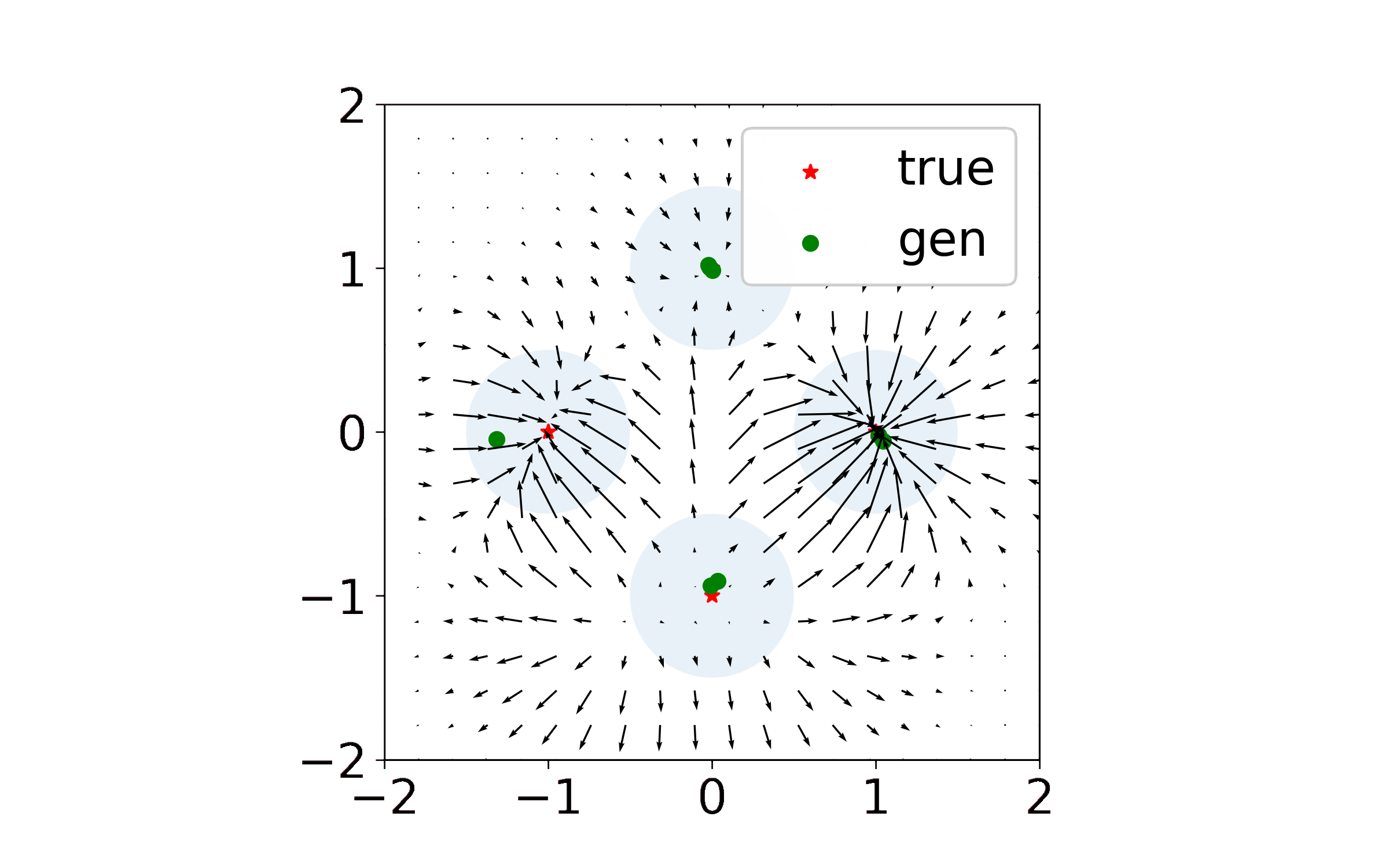
We made the simplifying assumption that our discriminator was a kernel machine and that our generator was directly parameterized by a set of points (similar to the Dirac-GAN of Mescheder et al. 2018). Generally we found that this framework, which we called the Isolated Points Model, allowed us to analyze local stability and convergence rates in terms of model hyperparameters such as kernel width and learning rates. Check out our NeurIPS paper for the full theory.

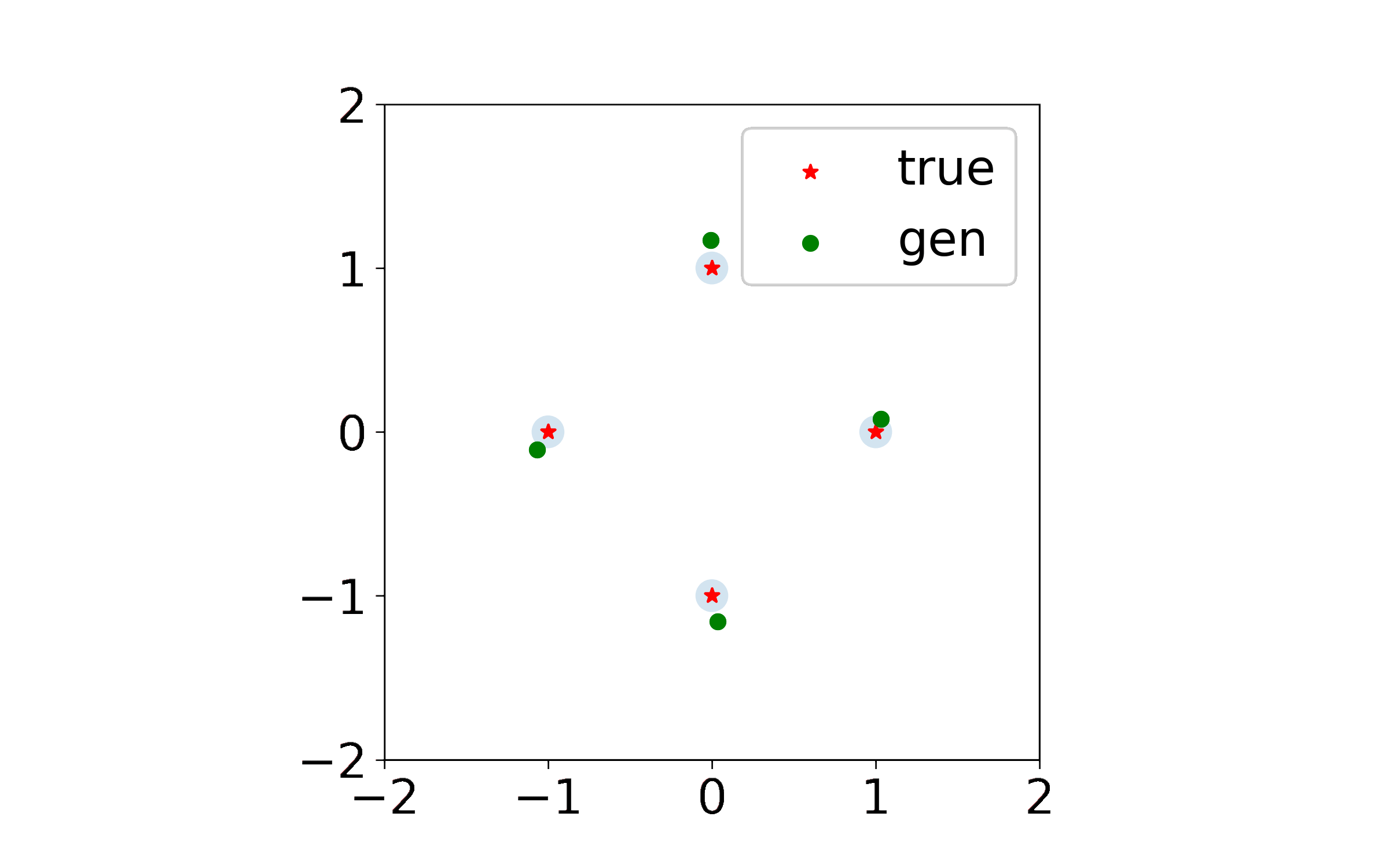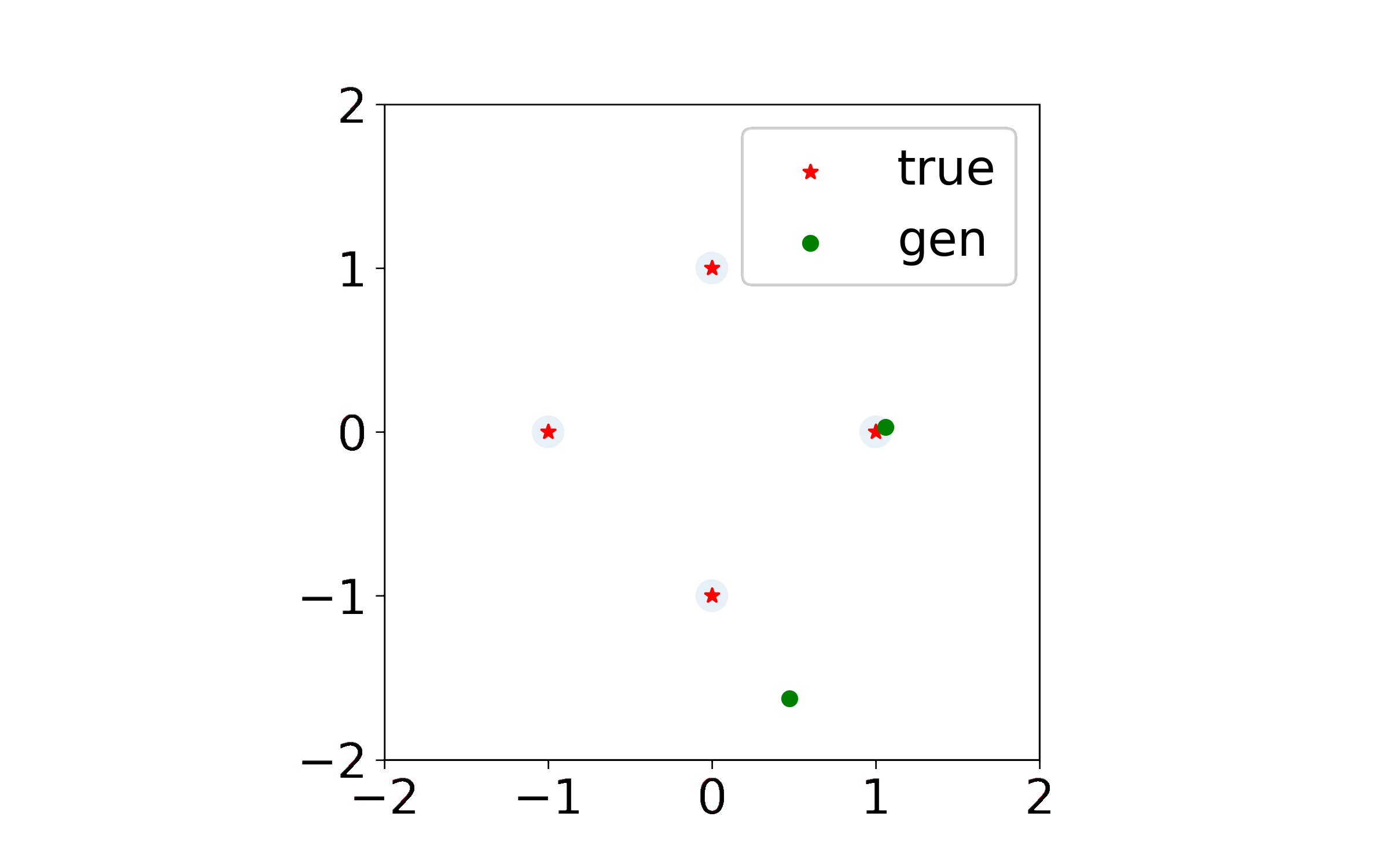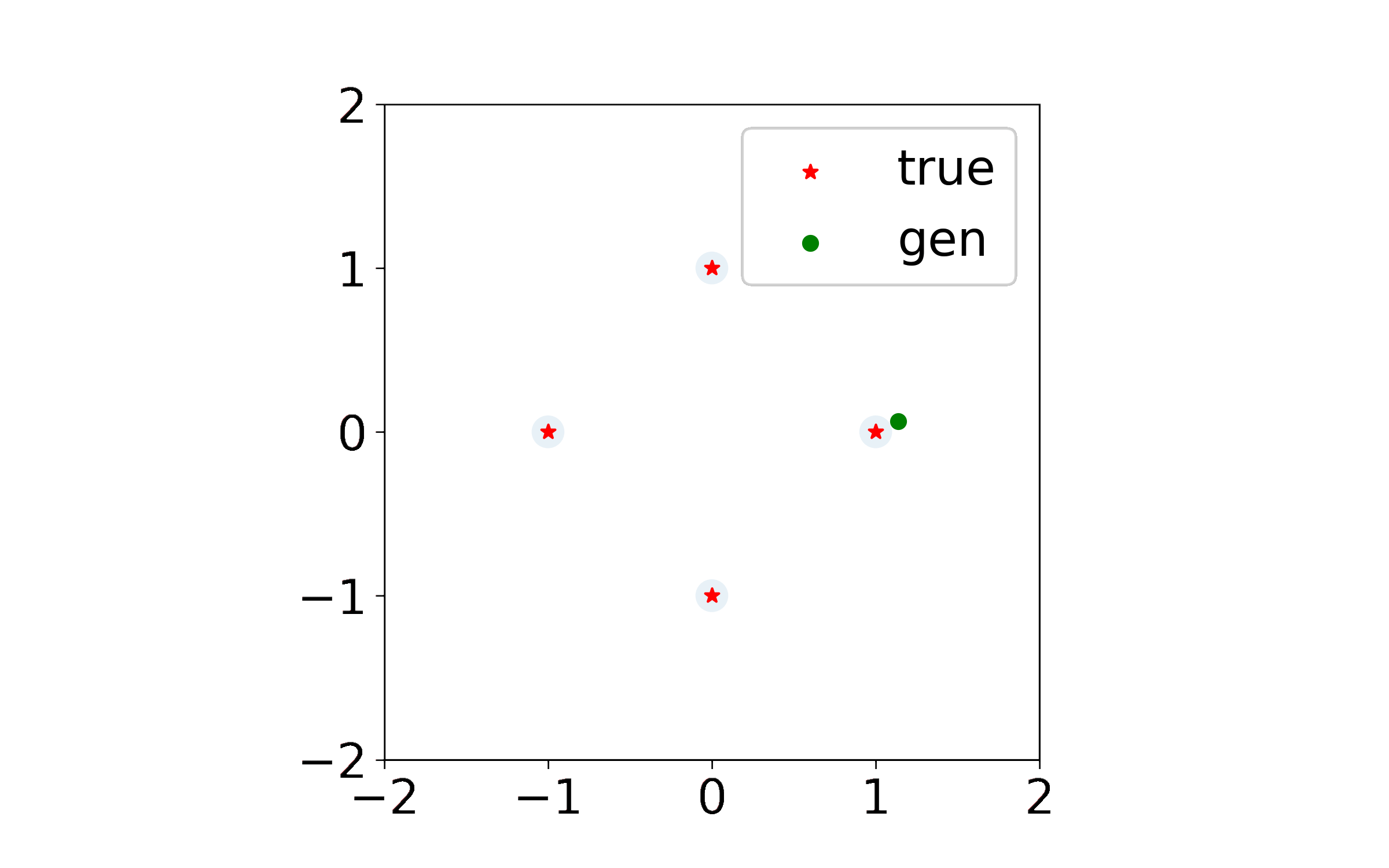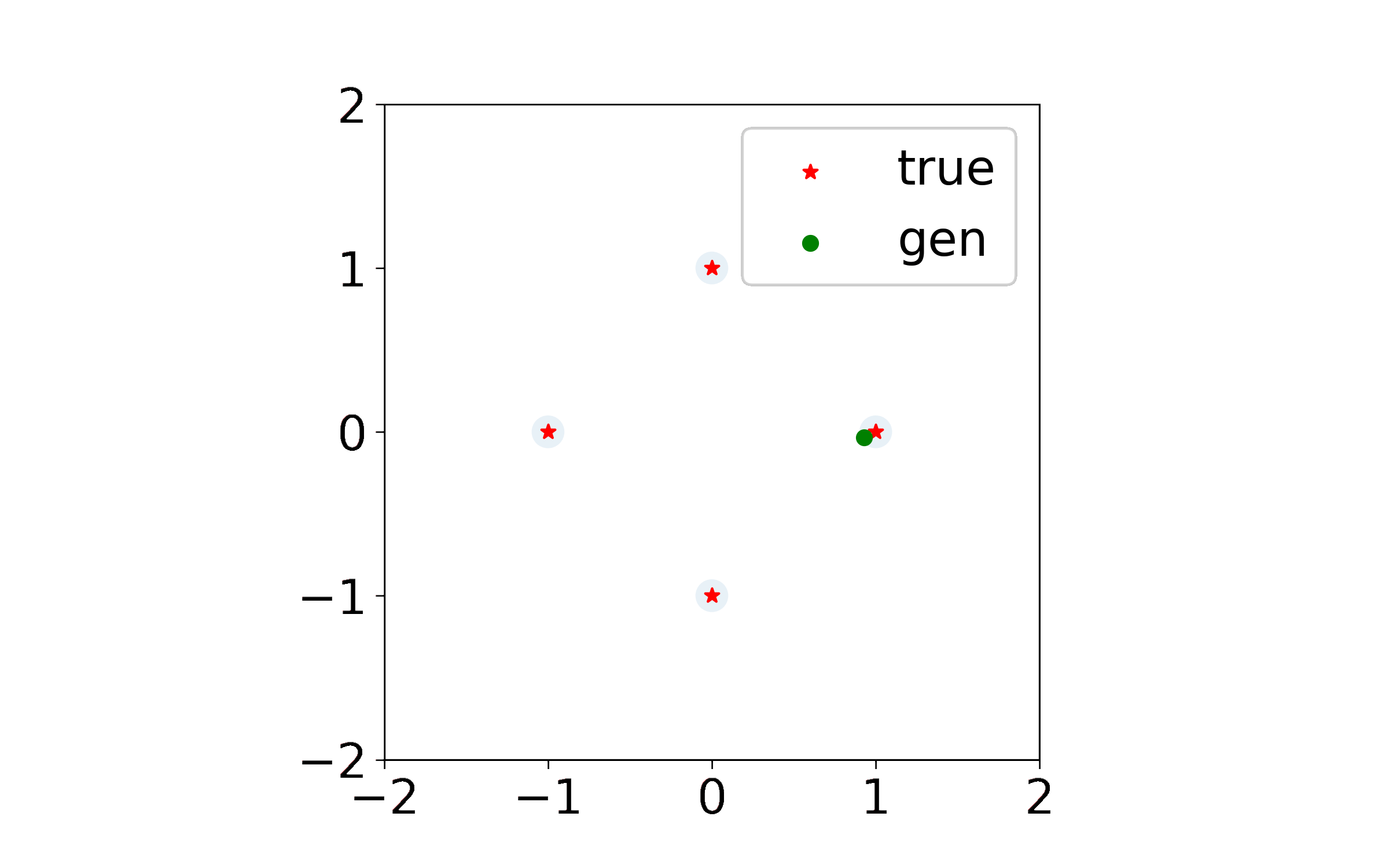
What I couldn’t easily add to the paper were animations of the generated point trajectories, which were quite pretty and which at times resembled some sort of exotic solar system. Indeed, when discriminator regularization is large enough, the dynamics begin to look like interactions between charged particles. I am using this page to share some of the more interesting simulations, and plan to add more in the future.

Simulations

Exact Kernel

Random Features Kernel